오늘은 전기장과 전기련선에 대하여 알아보자
전기장과 전기력선에 대하여

1. 전기장이란 ?

전기장 (Electric field)은 ‘어느 하나의 전하가 전기적인 힘을 미치는 공간’이라고 할 수 있다. 다시 말하면 어느 공간에 하나의 전하를 놓으면 주위에 있는 다른 전하에게 영향을 미치는 성질이라 할 수 있다. 여기서 ‘장(field)’에는 전기장 뿐만 아니라 중력장, 자기장 등도 있는데 예를 들어 자석에 쇠구슬을 서서히 다가가게 하면, 어느 일정한 거리에 도달하는 순간 자석이 쇠구슬을 끌어 당기면서 자석에 붙게 된다. 이는 자석이 가진 힘이 미치는 공간, 즉 장(field)에 쇠구슬이 진입했기에 쇠구슬이 자석의 힘의 영향을 받게 된 것이다.
이 예를 통해 ‘장(field)’이란 비접촉력을 설명할 때 사용하는 용어라는 것을 알 수 있다.

전기장도 마찬가지로 하나의 전하의 힘이 이웃한 전하에게 영향을 미치는 영역을 말한다.
위 그림에서 원전하 Q의 근처에 임의의 시험전하 q가 들어 왔다고 가정을 해 보자.
Q와 q가 모두 양전하라면 Q와 q는 서로 척력을 발생시키며 반발할 것이다. 그러면 반발력이 Q와 q가 서로 맞닿아 있을 때만 발생하는가 ? 그건 아니다.
전기장 (Electric field)이라는 성질은 공간적으로 떨어져 있는 곳에도 영향을 미친다는 의미가 포함되어 있으므로, Q와 q는 일정한 거리에 접근하는 순간 Q의 전기장에 의해 서로 닿지도 않았는데 반발력이 발생하게 된다. 만약에 Q는 양전하이고 q는 음전하라면 Q의 전기장내에 q가 들어서면 서로 끌어 당기는 인력이 발생할 것이다.
이러한 전기장을 식으로 표현할 때 E (전계의 세기)로 표현하며, 전기장을 알고 있을 때 전기력을 구하는 식은 다음과 같다.

이와 같이 전기장을 알게 되면 전기장 내에 있는 전하가 받는 힘의 크기와 방향도 알 수 있게 된다. 다시 말하면 전기장 (전계의 세기) E는 시험전하 q가 Q의 전기장 내에서 전기력을 받는 세기라고 할 수 있다.
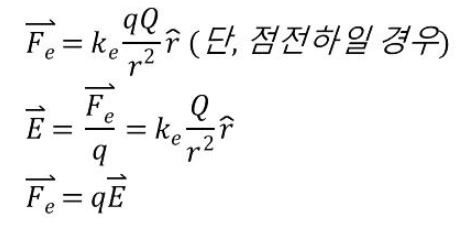
Q와 q가 점전하라고 한다면 전기력은 쿨룽의 법칙에 의하여 구할 수 있고, 이 식에서 전기장 (전계의 세기)을 구하는 식을 유도할 수 있다. 위 식에서 결국 전기장을 구하는 식은 쿨룽의 법칙, 전기력을 구하는 식에서 시험전하의 전하량 q를 빼면 된다.
위 식에서 이 전기장에 대하여 하나 덧붙이면, 전기장이 균일하게 분포되어 있다고 가정하면 전하량이 q이고 질량이 m인 입자를 균일한 전기장 E 내에 놓았을 때의 입자가속도를 구할 수 있게 된다.
※ 전기력 F는 단지, 힘의 종류 중에 하나이므로 뉴턴의 운동법칙 F = ma 의 식을 적용할 수 있다.

위와 같이 F = ma 를 이용하여 균일한 전기장 E 내에 위치한 전하 q, 질량 m인 입자의 입자 가속도를 구하는 방정식을 유도해 낼 수 있다. (단, 균일한 전기장일 때 입자에 작용하는 전기장이 일정하여 등가속도 운동임을 특정할 수 있다)
2. 전기력선이란 ?

전기력선 (Electric field lines)은 ‘전기장을 눈에 보이게 선으로 그려 놓은 것’이라 할 수
있다. 전기장을 형성하는 전기력선의 벡터를 선으로 이어 놓은 것이라 할 수 있다.

양전하, 음전하이냐를 떠나서 모든 전하는 자신만의 전기장을 갖게 되는데, 이 전기장은 눈에 보이지 않으므로 전기장이 미치는 범위와 형태를 선으로 표현하면 이해하기가 쉽게 된다. 가장 기본적인 전기력선은 위 그림처럼 양전하와 음전하의 전기장을 표현하는 것인데 음전하는 화살표가 안쪽으로 양전하는 화살표가 바깥쪽으로 향하게 된다.

이 때 전기력선의 규칙은 다음과 같다.
⊙ 전기장 벡터 E는 각 점에서 전기력선의 접선방향이다.
⊙ 전기력선은 양전하에서 나와서 음전하로 들어간다.
⊙ 전기력선은 서로 교차하지 않는다.

이러한 규칙에 따라 전기력선은 위 그림과 같이 다양한 형태로 나타난다. 전하 하나만 독립적으로 존재하거나, 같은 극성을 같는 전하가 이웃할 때, 다른 극성을 갖는 전하가 이웃할 때 등 전기력선이 나타는 모양을 각각 다르게 된다.
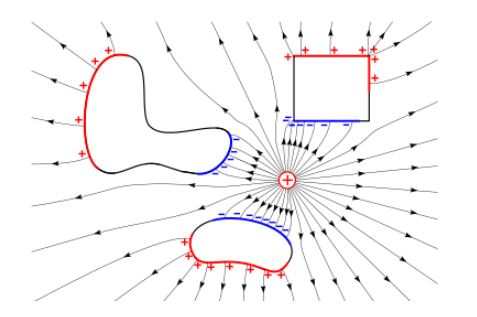
전기력선은 단순히 방향만을 알려 줄 뿐만 아니라 전기력선이 어떻게 분포되어 있느냐에 따라 전기장의 세기도 가늠할 수 있다. 전기력선이 듬성듬성 분포한 곳은 상대적으로 전기장이 약한 곳이며, 전기력선이 촘촘히 분포한 곳은 전기장이 상대적으로 강한 곳이다.
그런데 지금까지는 전하가 각각 하나씩 존재하는 경우를 가정했는데 현실 세계에서는 전하가 하나의 공간에 무수히 많이 존재하게 된다. 한 공간에 전하가 무수히 많이 존재하게 되면 각 전하가 가진 전기장이 서로 중첩될 수 있는데 이럴 경우 특정지점의 전기장 E는 그 주변에 존재하는 무수한 전하들의 전기장들의 벡터합으로 표현할 수 있다. 이를 중첩의 원리라고 하며 식으로 표현하면 다음과 같다.

